Leandro C. Gallo, Ernesto O. Cristallini, Renata N. Tomezzoli
2 017
Latinmag Letters, Volume 7, Special Issue (2017), PM07, 1-5. Proceedings Juriquilla, Qro, Mexico
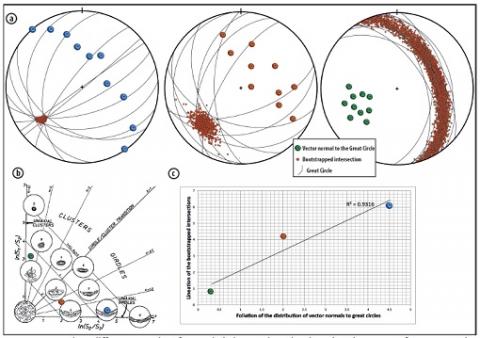
Dado el sesgo documentado en el cálculo de la intersección de círculos máximos de remagnetización como función del paralelismo de los mismos, y que el mismo es elongado en la dirección de paralelismo, se encuentra que la asunción de simetría rotacional (i.e. estadística de Fisher) alrededor de la intersección medida, parecería ser insuficiente para abordarlo. En esta contribución, se aborda la intersección de círculos máximos a partir del método “bootstrap” de las mismas. Cálculos repetidos exploran los posibles resultados numéricamente; intersecciones sesgadas debido al paralelismo de los círculos máximos tendrán una distribución elongada de las intersecciones re-muestreadas. El método calcula una región de confianza basada en la distribución empírica de las intersecciones re-muestreadas. Una versión preliminar del programa descripto se encuentra disponible a pedido.
Given the already documented bias in the determination of intersecting remagnetization great circles
as a function of the parallelism of the circles, resulting in an elongated bias in that direction, we found that rotational symmetry assumptions around the intersection would seem to be insufficient. In this contribution, we address the intersection and its inherent bias by doing bootstrap. Repeated calculations explore possible outcomes numerically; elongated distributions of the bootstrapped intersections are regarded as biased. The method calculates a more realistic confidence region based on the empirical distribution of the bootstrapped intersections. A preliminary version of the program implementing the method described here is available from L. Gallo on request.
as a function of the parallelism of the circles, resulting in an elongated bias in that direction, we found that rotational symmetry assumptions around the intersection would seem to be insufficient. In this contribution, we address the intersection and its inherent bias by doing bootstrap. Repeated calculations explore possible outcomes numerically; elongated distributions of the bootstrapped intersections are regarded as biased. The method calculates a more realistic confidence region based on the empirical distribution of the bootstrapped intersections. A preliminary version of the program implementing the method described here is available from L. Gallo on request.
http://igeba.gl.fcen.uba.ar/Files/Publicaciones/Publicacion-Tomezzoli-Bootstrapped intersecting.pdf